Sara Ghotb

X-Ray diffraction

X-Ray diffraction is a technique used to determine the atomic and molecular structure of materials. In crystal, atoms are placed align with each other and they have regular spacing where this spacing is about 10 A. The general process that happens in XRD is look exactly like diffraction. The wavelength of the visible light is about 400 - 700 nm which is way bigger than the crystal spacing so we can not have this diffraction in the crystal with the visible light. However, if we can find a wavelength comparable to the atomic spacing 10 -10 m we can get a lot of information about the crystal by having the reflection in the crystal. As a matter of fact, x-ray light has this similar wavelength and this whole process is called X-Ray diffraction. Note that, we only get x-ray diffraction in the crystalline structure and there is no diffraction pattern for amorphous structures since they don't have any regular spacing.

BRAGG'S LAW

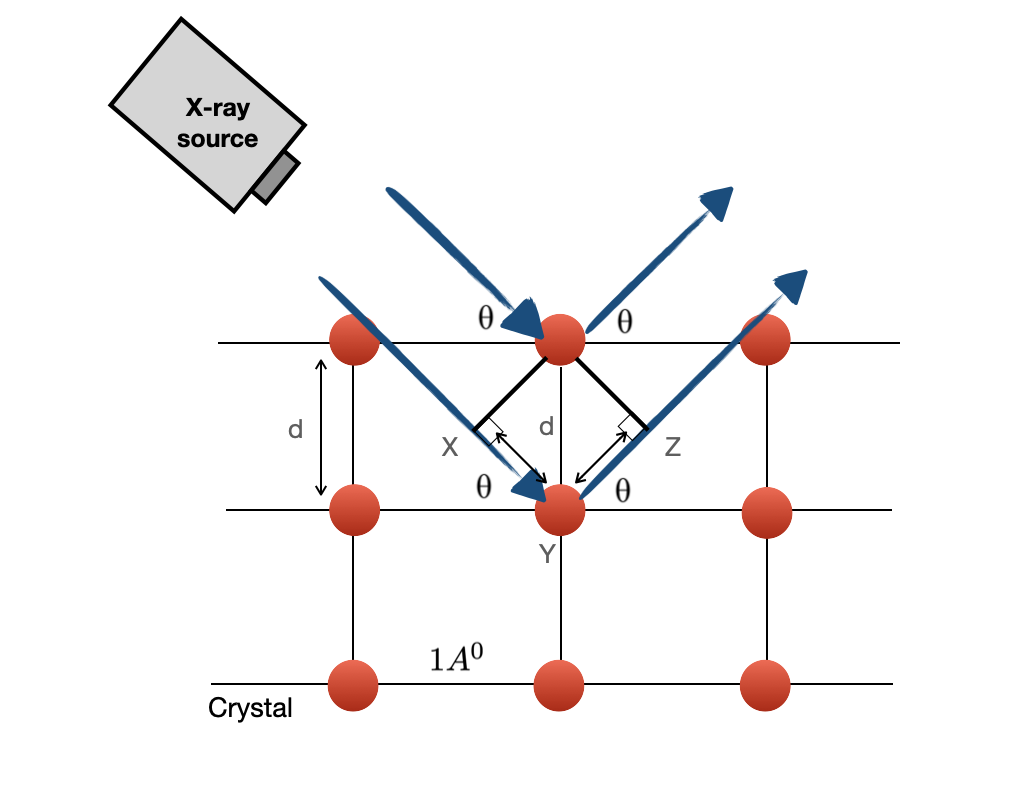
The Bragg's law is useful for measuring wavelengths and for determining the lattice spacings of crystals. Bragg's equation is given by: $$nλ = 2dsin(Θ)$$ Where λ is the wavelength of the radiation, d is inter-planar spacing between the atoms and Θ is the angle between the incident (or diffracted) ray and the relevant crystal planes and n is an integer referred to the order of diffraction. The basic idea behind Bragg's law is that when this law is satisfied, X-ray beams scattered from successive planes in the crystal (as shown) will travel distances differing by exactly one wavelength. In another word, if the difference between the distance travelled by the beam is nλ the Bragg's law is satisfied. X-rays scattered from successive planes will interact constructively when they eventually reach the X-ray detector and we will see the peak.

WHY RECIPROCAL LATTICE?

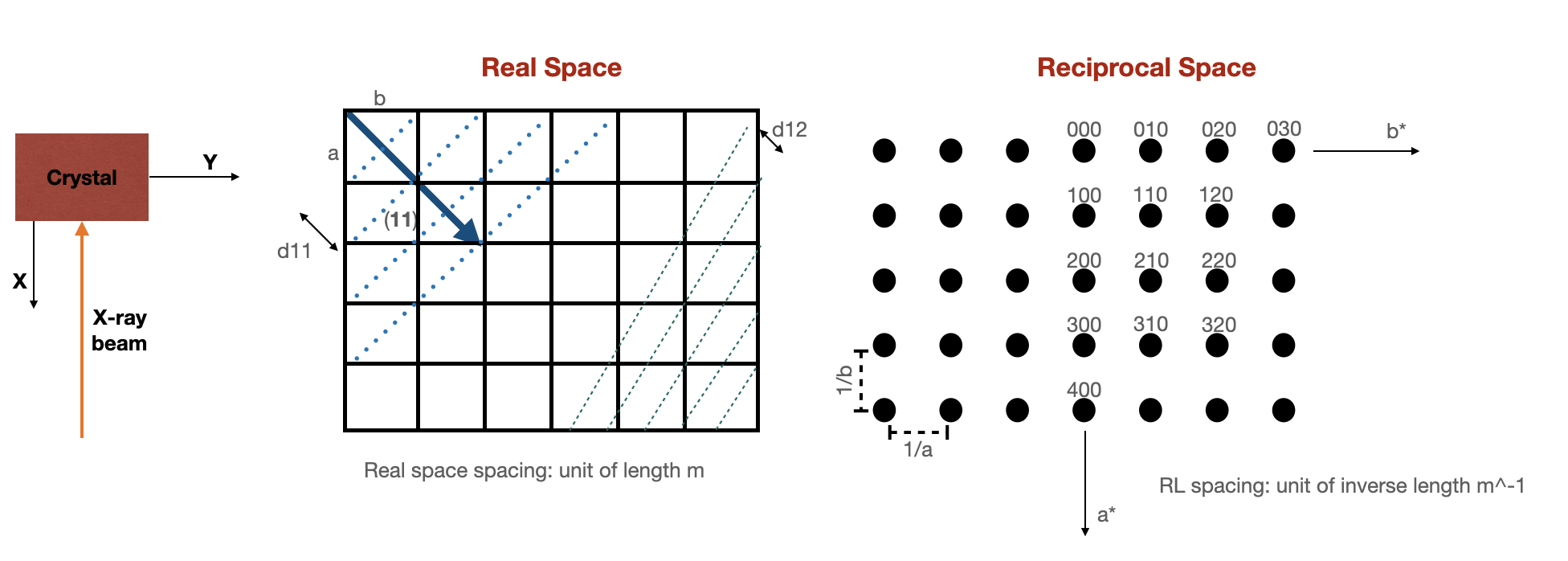
When we talk about real space, we are talking about spacing between one lattice point and for each family of planes we have d spacing which separates one member of that family from another member of that family. Note that all of these in real space are given in unit of distance(m). In reciprocal space each point represents family of planes. For example the distance from the origin to the point for example (11) is given by one over d spacing of 11 family of planes in the real space.

Note that all of these in reciprocal space are given in unit of inverse length(m−1). If the lattice spacing between family of planes in real space is smaller this means in reciprocal space the distance from origin to that family of plane is larger. In XRD what we are interested in, is the interaction of x-ray beam with a particular beam orien- tation.

Ewald sphere

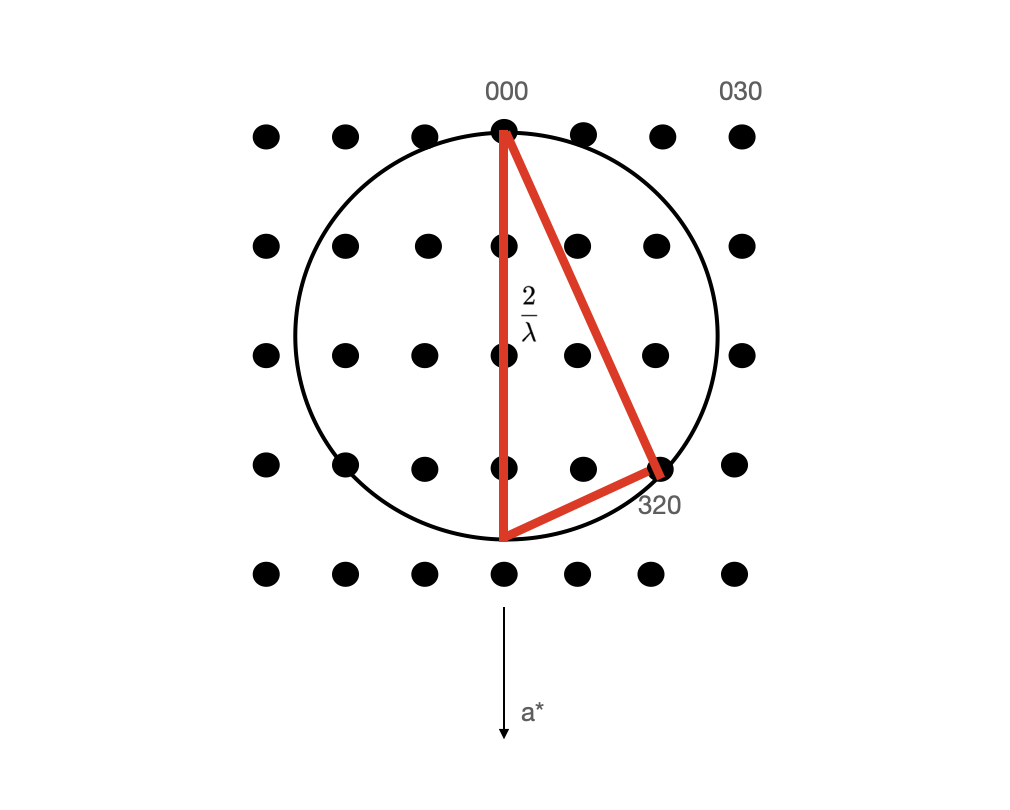
After creating our reciprocal lattice, we define a sphere that has a very particular diameter λ2, where λ is the wavelength of the radiation and it sits at the origin of the reciprocal lattice along the incident beam. When this sphere intersects with the lattice point that’s when the diffraction condition is met.

sin(Θ) = λ/2d

λ = 2dsin(Θ)

nλ = 2dsin(Θ)

So it gives us the standard Bragg's law. So this means the Bragg's law is satisfied when a reciprocal lattice points sits on the Ewald sphere. Now let's ask ourselves what will happen if we rotate our crystal? If we rotate our crystal we rotate our reciprocal lattice as well. Just on some special points this reciprocal lattice points are going to be on the Ewald sphere and Bragg's law is going to be satisfied for that point. The angle in the figure is 2Θ angle and it shows the crystal orientation. So at different crystal orientations, different planes satisfy Bragg’s law and all 2Θ angles are dif- ferent. Note that in 3d all is more complex since lattice is going to be 3d and it is going to be sphere instead of circle.

XRD DEVICE

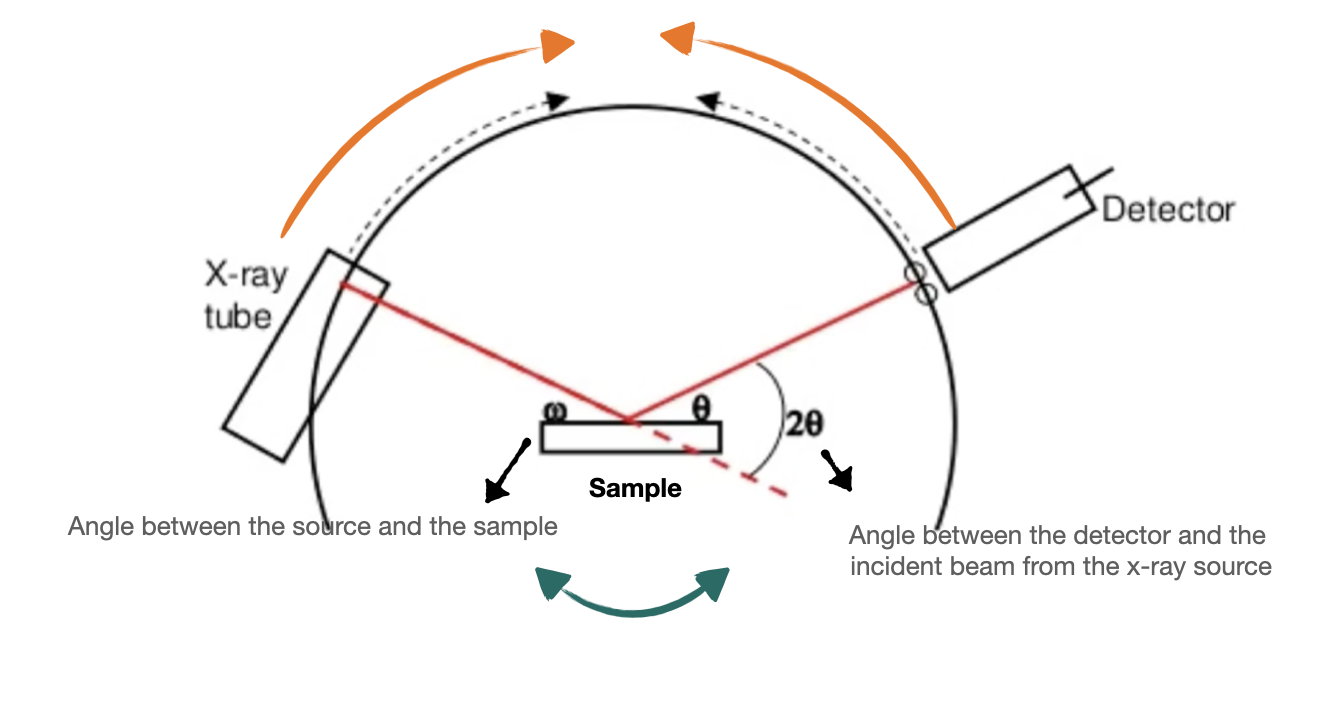
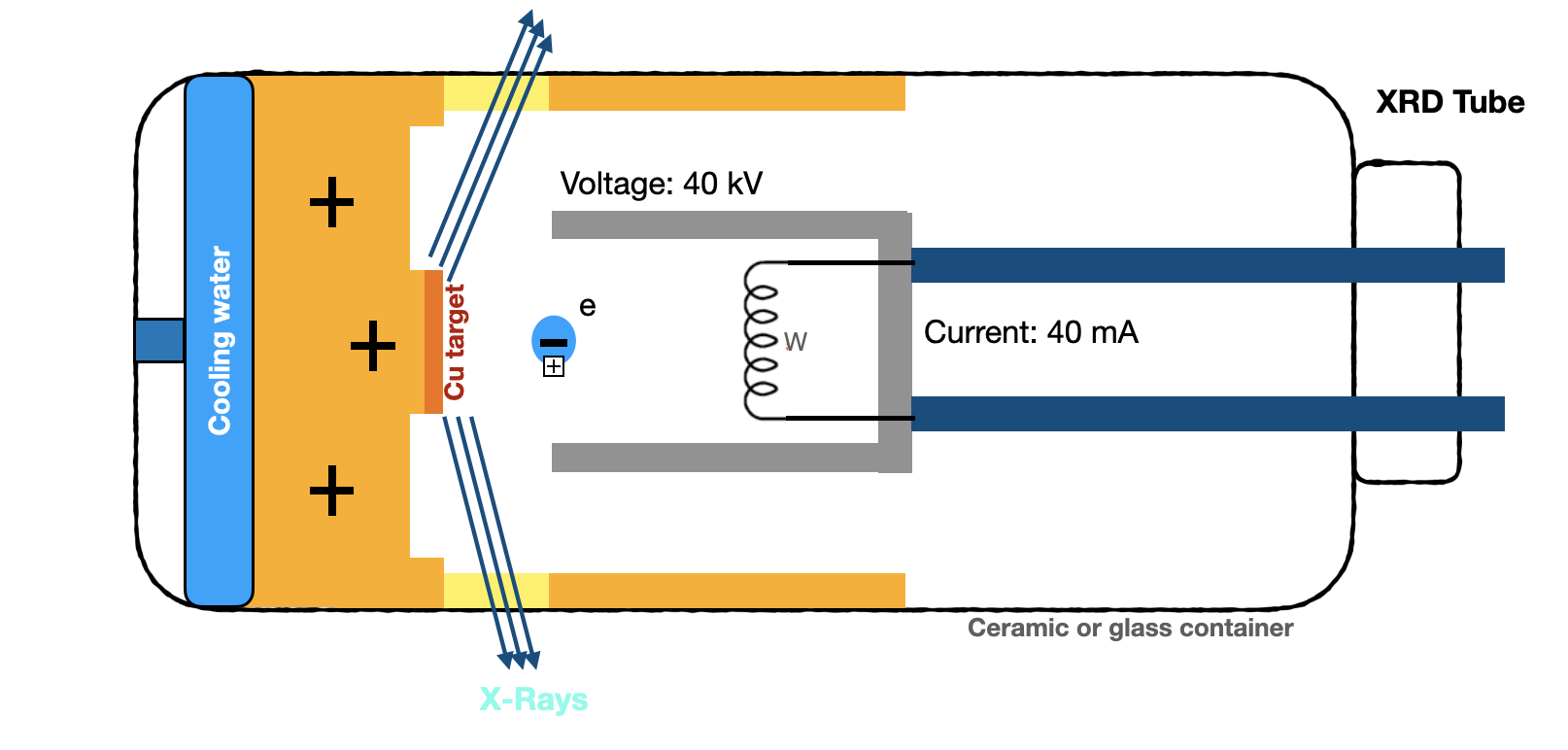
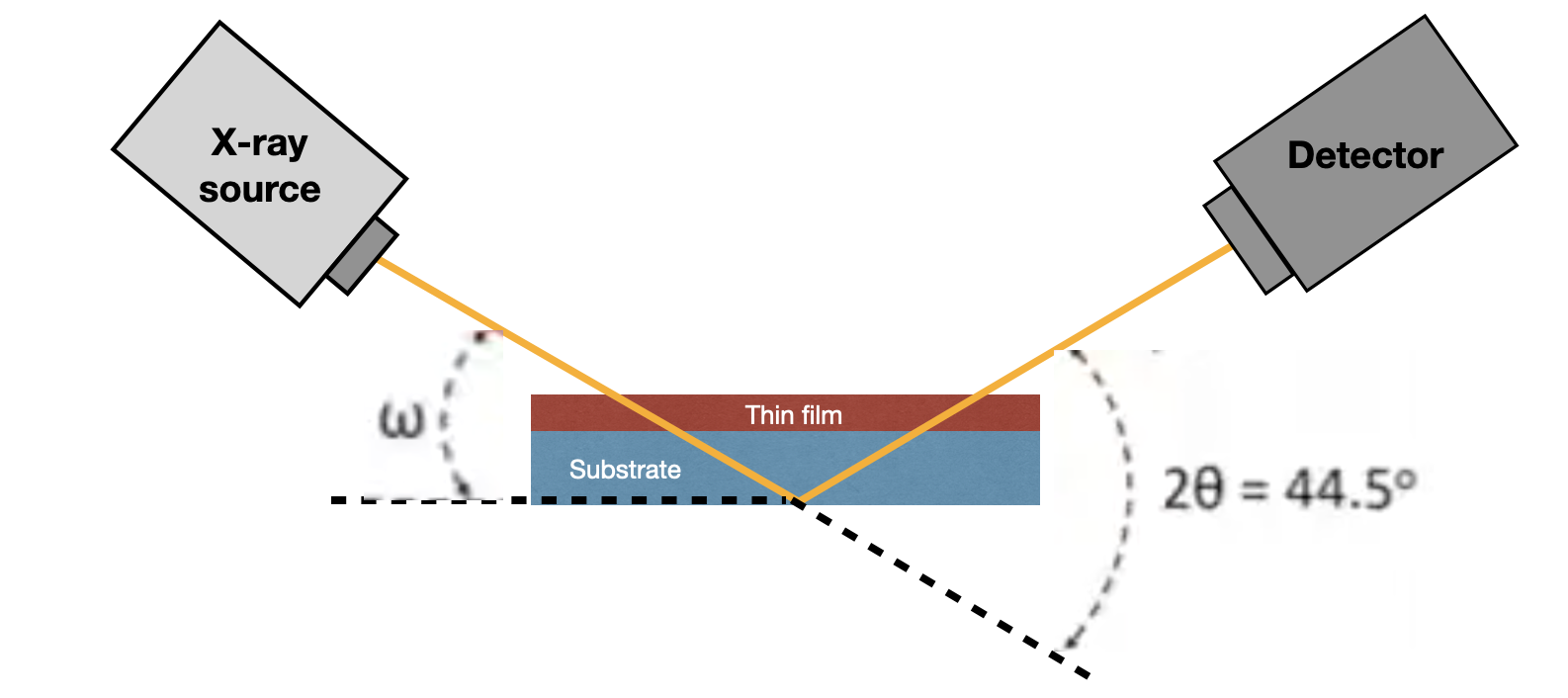
There are several kinds of XRD machines, most of them has fixed source and detector and sample is rotating and for others the sample is fixed and the source and detector are rotating which our XRD machine in the lab belongs to the second group. The advantage of having source and detector rotating and fixed sample is that there is a possibility of losing the sample while the rotation. The most important parts of the XRD machine are x-ray source, detector and the sample holder. The angle that is formed between the source of the x-ray and the sample is ω and the angle that is formed between the detector and the incident beam from the x-ray source is 2Θ, which means it’s double the ω angle.

HOW X-RAY IS GENERATED IN THE XRD MACHINE

An applied current (in our case 40mA) heats up Tungsten filament that acts as a cathode, which liberates electrons. These liberated electrons are accelerated by high voltage and hit the Copper target where Copper x-rays are generated. The reason that we use Copper target is that X-ray radiations of Cu are comparable to the atomic distancing. Then the x-ray exits the tube and are incident on the sample from which they are diffracted into a scintillating type detector.

• Slit

The beam passes through the slit which determines the angular width of the beam. Wider slit give more energy but have wider peaks, smaller slit gives less energy but better resolution.

• Nickel Filter

The beam also passes through the nickel filter, the nickel filter removes the k-beta energy for diffracted beam that enters the detector.

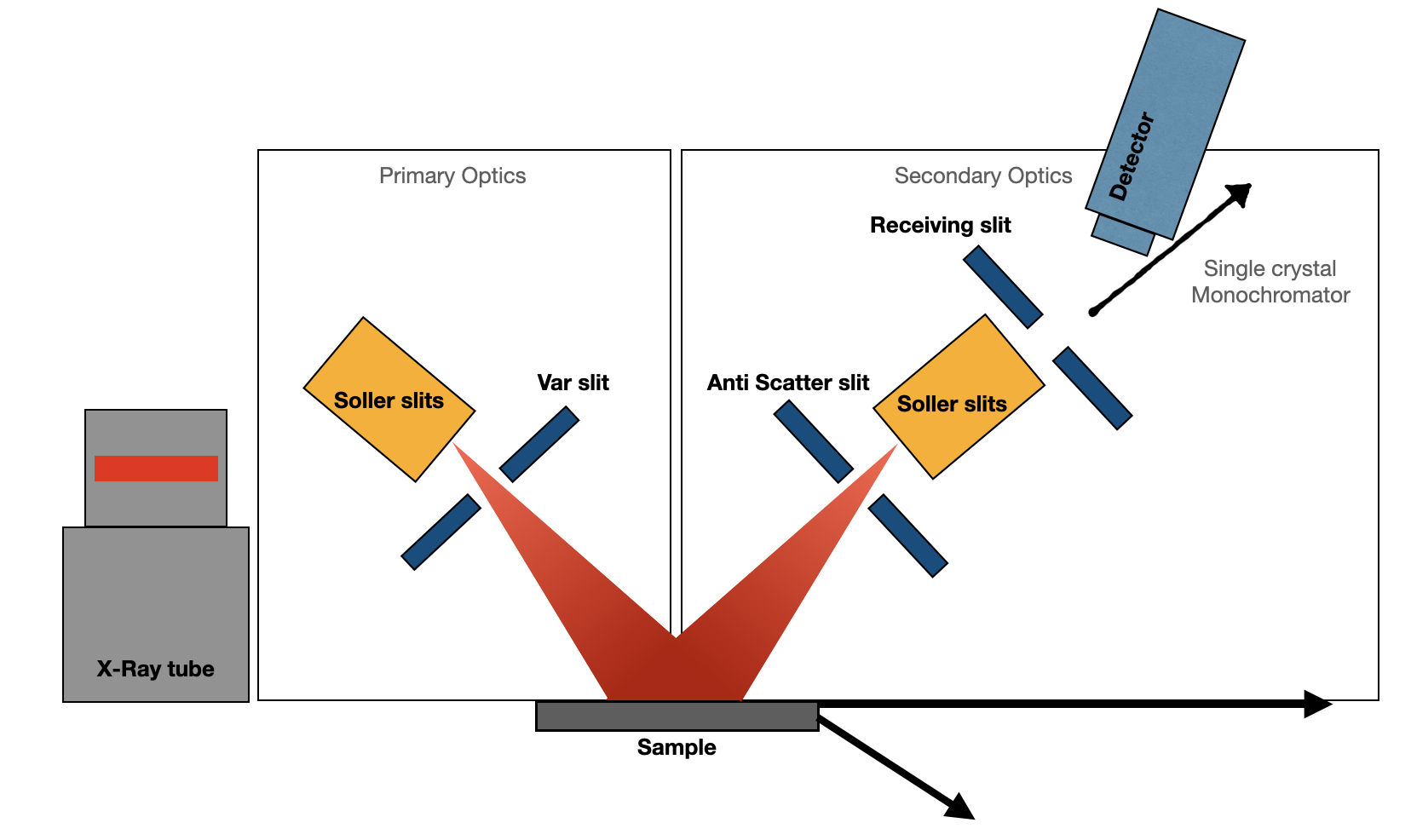
Xrd device consists of two optics, primary optics and secondary optics. Primary optics condition the x-ray to be more efficient. The primary optics conditions the x-ray beam before it hits the sample and the secondary optics retrieves the x-rays that are reflected by the sample before they go through the detector.

Primary Optics :

Primary optics can be broken down to three main parts.

1. Soller slits:

Soller slits keep beams in a correct plane. These slits are metal foil stacked at a constant interval between. Soller slits helps beam to be in a correct path.

2. Divergence slit:

Divergence slits control how wide the beam is. Divergence slit blocks X-rays that have too great a divergence. Divergence slits come in many different sizes, and the size of the divergence slit influences the peak intensity and peak shape. For example a narrow divergence slit (var slit):

• Reduce the intensity of the x-ray beam.
• Produce sharper peaks.
• Reduce the length of the X-ray beam hitting the sample.
• The instrument resolution is improved so that the closely spaced peak can be resolved.

Var slit in the primary optics in our device can be changed manually, however, the divergence slit at the secondary optics for the detector is changing by computer.

3. The monochromators:

The monochromators filter the unwanted X-ray beams which only allows kα1 and kα2 radiations to pass and it filters out any white radiation or kβ radiation. The monochromator and divergence slit greatly increase the resolution of data. The monochromator in our xrd device in primary optics has two different type, one for powder measurement and the other for the thin film.

Secondary Optics :

Secondary optics are the receiving end of x-ray that are diffracted by the sample and they can be broken down to four main parts.

1. Selection slit (anti-scatter slit)
2. Soller slit
3. Receiving slit
4. The monochromator (kβ filter). (Filters kβ rays and white radiation)

DIFFERENT TYPES OF MEASUREMENT

There exist different kind of XRD measurements on thin films, where the angle between source and detector are different. Let's take a look into each.

1. Bragg-Brentano XRD (XRD)

   In this conventional Bragg-Brentano xrd measurement X-ray source and detector move and it may probe too deeply beneath the surface of your study material that interests you. This means it can mostly diffract from the substrate rather than the film, in other word x-ray interact with the substrate much more than thin film. In this type there is a weak contribution from the thin film and strong contribution from the substrate.


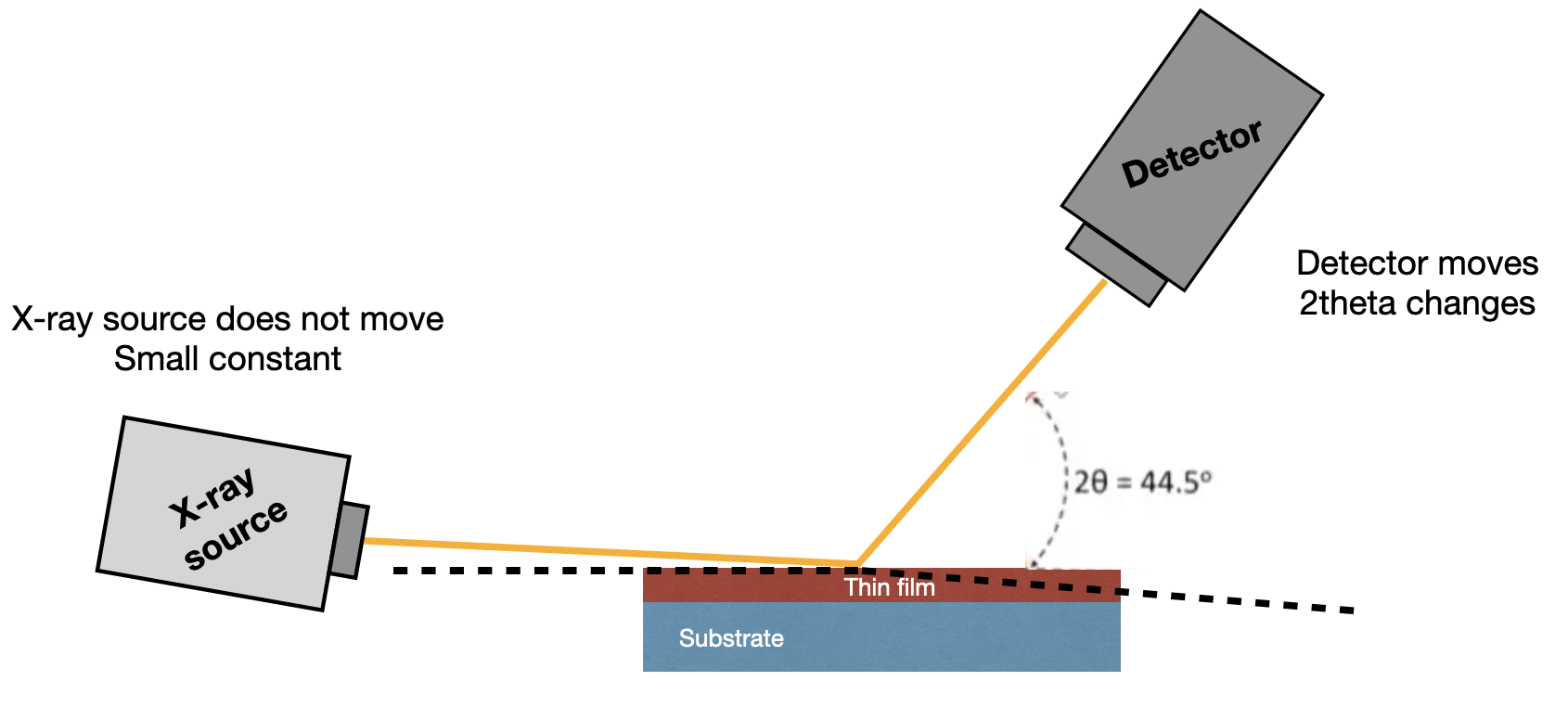
2. Grazing Incident XRD (GIXRD)

   In this type it is possible to hold the incident x-ray constant while the detector rotates through 2Θ. In another word in this experiment the penetration depth of the incident ray is kept constant. Grazing incident xrd can give us the larger with higher intensity peaks than the conventional xrd. By decreasing the incident beam or ω we can get more reflection from the film rather than substrate and by decreasing this angle we get larger peaks however, there is an angle where x-ray no longer penetrate into the material and you no longer see any peaks. So there is a limitation for decreasing the angle.

OUTPUT OF THE XRD

The result of xrd can be seen in a graph intensity vs 2Θ. There are several factors that you see in the xrd data, peak position, intensity and the peak shape.

1. Peak position

Peak position depends on the instrument parameter such as wavelength. So, the Bragg’s law is used to relate this position to material peak position that is instrument independent. The spacing of the peaks can be used to define a crystal cell unit because the distance between the diffracting plane of an atom determines the peak position.

2. Peak Intensity

Peak intensity is based on counts which is the number of x-rays detected for a given peak position. The intensity is determined by the atoms that are present in the diffracting angle. So intensity gives insights on the elements that are present in your sample.

3. Shape of the peak

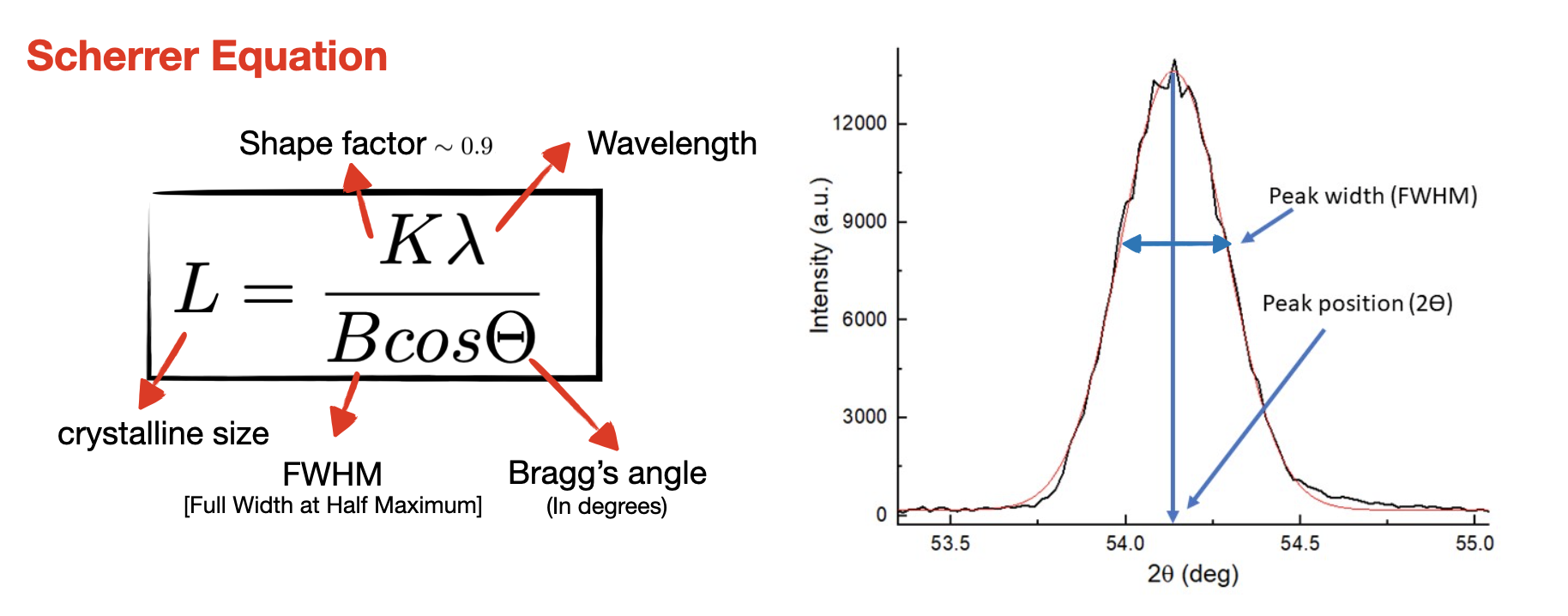
XRD takes into account the shape and the width of the peak using the Scherrer equation which depends on peak width and the crystallite size. L= Kλ/BcosΘ In this equation L is crystalline size, K is shape factor ∼ 0.9, λ is wavelength, B is FWHM of the peak and Θ is Bragg angle in degrees. Each diffraction spectra is like a finger print. In result of xrd each peak is associated with a particular family of plane and that family of plane has a particular d spacing.