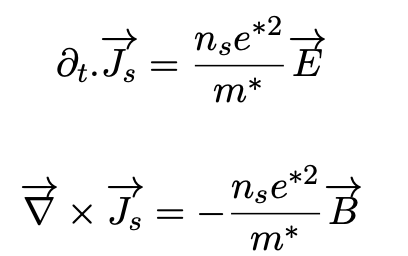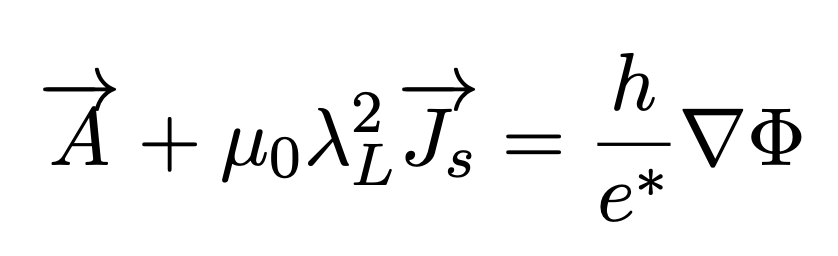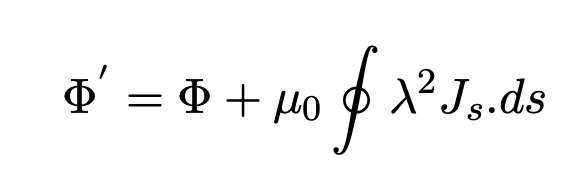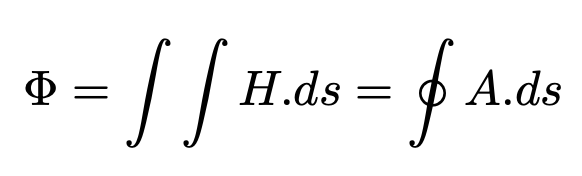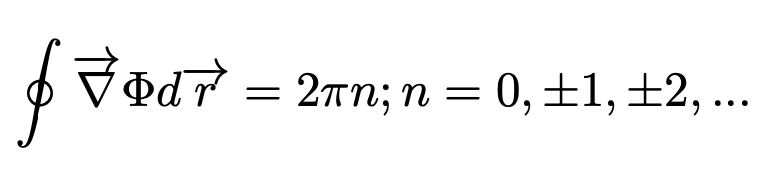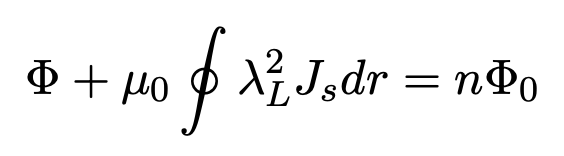Sara Ghotb

What is Little-Parks effect?

The Little- Parks (stroke-linecap) experiment measures the resistance of a nanoring close to its transition temperature as a function of applied magnetic field. It is used to detect resistance oscillations as a function of the magnetic field with a single field period set by the size of the ring and the charge of the supercurrent carriers. For conventional superconductors, the charge is always q = -2e for the electron pairs. However, there are theoretical models predicting different values for superconducting copper-oxygen materials (cuprates) in different doping regimes. Up to now, at optimal doping with the maximum critical temperature, the existing measurements with YBa2Cu3O7 nanorings have also shown q = -2e. Since our expertise lies rather in Pr2-xCexCuO4, the electron-doped cuprates, we propose to explore the Little-Parks effect on this material as a function of doping.

Before jumping to Little-Parks effect we need to first understand the concept of fluxoid. London for the first time introduced the concept of fluxoid associated with each hole passing through a superconductor.

Fluxoid quantization

One of the important phenomena that shows an evidence of a macroscopic quantum behavior in superconducting materials happens at multiply connected superconductors like superconducting rings or superconducting cylinders where there is a flux quantization. London for the first time introduced the concept of fluxoid associated with each hole passing through the superconducting material. Before start to introduce the concept of fluxoid, first lets review London equation. Where first term is ordinary flux and the second term is for screening current part. If the loop is taken in the interior of a bulk sc where the current is zero the fluxoid equals to flux. So for a loop enclosing purely superconducting material the integration in the second term vanishes everywhere inside the loop and the fluxoid would be have to zero. However, if there is a physical hole or normal- non-sc material (where London equations are not valid) the deduction that Φ = 0 is not valid any more. One can show that the fluxoid has the same value for the same value for any loop in the sc enclosing the same non-sc spot and that value remains constant and the fluxoid is quantized in units of hq where q is the charge carrier and there are experiments that are designed to determine this q. Frietz and Heinz London developed two important equations which relates the current to the electromagnetic field in superconducting materials.

in these equations Js is the superconducting current density and the E and B are respectively electric and the magnetic fields within the super- conductor. Also by looking at these equations it can be realized that the constant part looks like the London penetration depth. So, obviously critical current density and superconductivity coherent length and penetration depth are related.

From the second Ginzburg-Landau equation we can write:

If we want to apply this equation on a closed line path around a hole in the superconductor we will have:

In this formula Φ is called fluxoid which is the sum of two terms, where Φ is the ordinary magnetic flux enclosed in the area surrounded by the closed loop and the term associated with the screening current. So from the definition of an ordinary flux in the loop, we have:

Fluxoid (Φ) is zero if we have purely superconducting material. So if the path encloses no hole and only superconducting material, fluxoid is going to be zero and the London equations are valid. However, as soon as we have a hole or any non superconducting material in the system fluxoid is not going to be zero. Φ has a unique constant value for all contours enclosing any given hole, which London predicted that this value should have a discrete set. In order to understand better this equation lets look at it more closely.

If the loop which is taken in the interior bulk of the superconductor where the current is zero (Js = 0) the second term in the equation is zero and fluxoid is going to be equal to flux. Also, for the loop enclosing the purley superconducting material the Meisner effect exclude all the magnetic field from the material and the fluxoid is going to be zero.

Depending on the temperature and the value of the magnetic field, the order parameter will alter between zero and one. So the value for fluxoid is going to be zero inside the superconductor. However, if we have a physical hole or non superconducting material (where the London equations are not valid anymore) inside the superconducting material the deduction that fluxoid is zero is not hold anymore and two terms in the equation exist and they are both important.

So one can show that fluxoid has the same value for any loop in the super- conducting material enclosing the same non superconducting spot. In order to show that fluxoid is quantized, from the fluxoid equation, the integral on the right side over the full path must be integer multiple of 2π in order to have the order parameter, single valued.

So the equation writes as:

Where, Φ0 = h = 2.07 × 10−7G − cm2 is the flux quantum for pair. This 2e equation describes flux quantization. From this equation one concludes that, if the integration is on the part that the screening currents are negligable, then the total magnetic flux through a superconducting loop is quantized in units of flux. (This equation is equivalent to the Bohr-Sommerfeld quantum condition). After London prediction of fluxoid, different experiments have shown that the flux which is trapped in a multiply connected superconductors is multi- ple unit of hc/2e.